Recurrent Independent Mechanisms

Like all ambitious papers, "Recurrent Independent Mechanisms" by Anirudh Goyal, Alex Lamb, Jordan Hoffmann, Shagun Sodhani, Sergey Levine, Yoshua Bengio, and Bernhard Schölkopf begins with an introduction that's one part motivation and one part philosophy. To motivate the Recurrent Independent Mechanisms (RIMs) model architecture, they first make a series of broad observations:

The world is governed by physical laws and has underlying structure
Isolated rules (independent mechanisms) are often sufficient to explain variation within a subsystem
Most mechanisms do not interact highly with each other (Newton's law of gravitation explains a particular phenomenon well, as do ideal gas laws, but we don't frequently have to model the interactions between the two)
Only a small subset of all mechanisms are relevant for any particular problem of interest

They also lay out some "desiderata" that inspired the design of the RIM architecture. In the main paper it's relegated to the Appendix, but I find it useful to think about high-level features present in the architecture up front:

1. Competitive Mechanisms

Competition gives us a means to allocate scarce resources and enforces sparsity. Part of the intuition here is that unless a mechanism is dominant for a given input, it may simply add noise to the system without meaningfully contributing (harming generalization). We're looking for a small number of strong correlations rather than a large number of weak ones.

2. Top Down Attention:

High level representations should modulate the way that future low-level inputs are processed. As humans we form expectations based on previously processed inputs. These expectations influence processing of future inputs and help selectively allocate perceptual resources.

An example of Top-Down processing can be seen in how we process the visual illusion known as the "Necker cube":

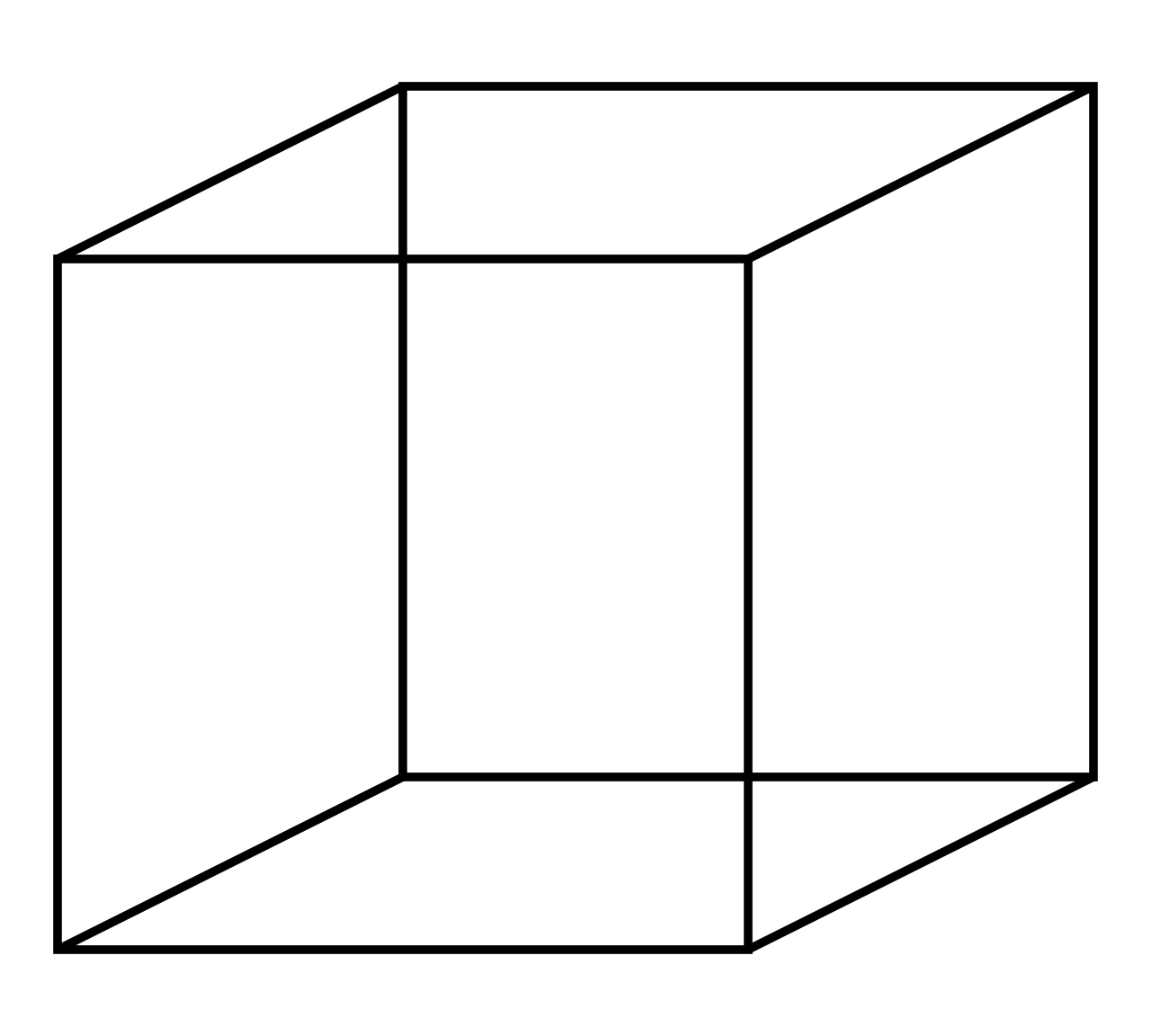
Image credit of https://en.wikipedia.org/wiki/Necker_cube

First, even though the "Necker Cube" is a 2D drawing, we perceive it as a cube. The prior expectations we have from living in a 3D world influence our perception of this 2D drawing. Secondly, there are two possible perspectives you can see the 3D cube from, and with a bit of focus you can view either of two squares as the front face of the cube. Although the drawing is ambiguous, we interpret all of the low-level visual inputs as being consistent with the higher-level representation we expect.

3. Sparse Information Flow:

Many model architectures assume interactions between all elements by default. In contrast RIMs assume that most other mechanisms outputs are irrelevant to a given mechanism.

4. Modular Computation Flow:

Mechanisms should be simple (low parameter count) and interact primarily with themselves (independently of other mechanisms).

What variety of machine learning architecture might satisfy these desiderata and exploit these observations well? What architectural decisions will give rise to independent mechanisms that interact sparingly? Enter RIMs.

A Recipe for RIMs

Ingredients:

\(k\) LSTM RNN's, each with it's own set of parameters (a RIM)

LSTM diagram from Chris Olah's fantastic blog

2 Key-Value Attention Layers

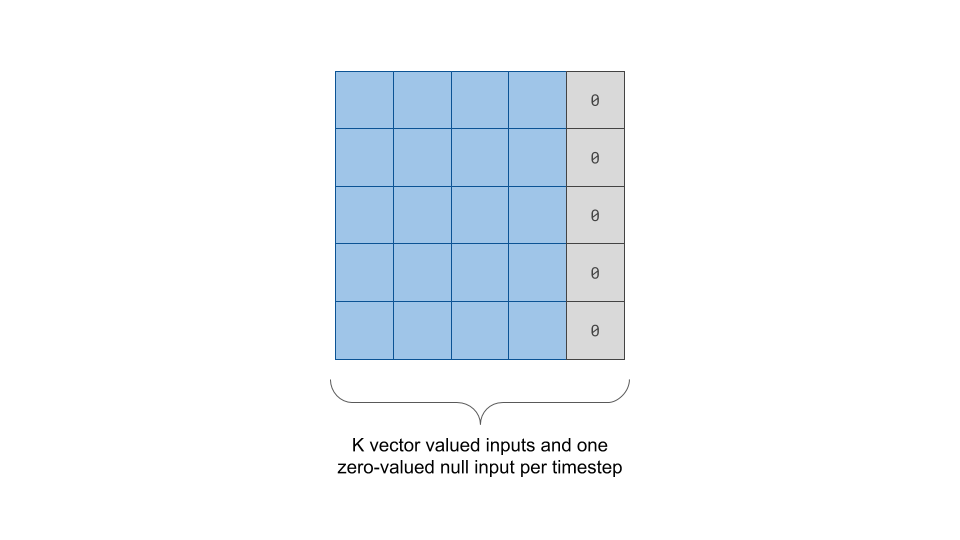
The computation performed by a typical key-value attention operation

Per timestep, \(k_{T-1}\) vector valued inputs and 1 zero-valued vector representing a null element, concatenated into a \(k_T, d\) matrix

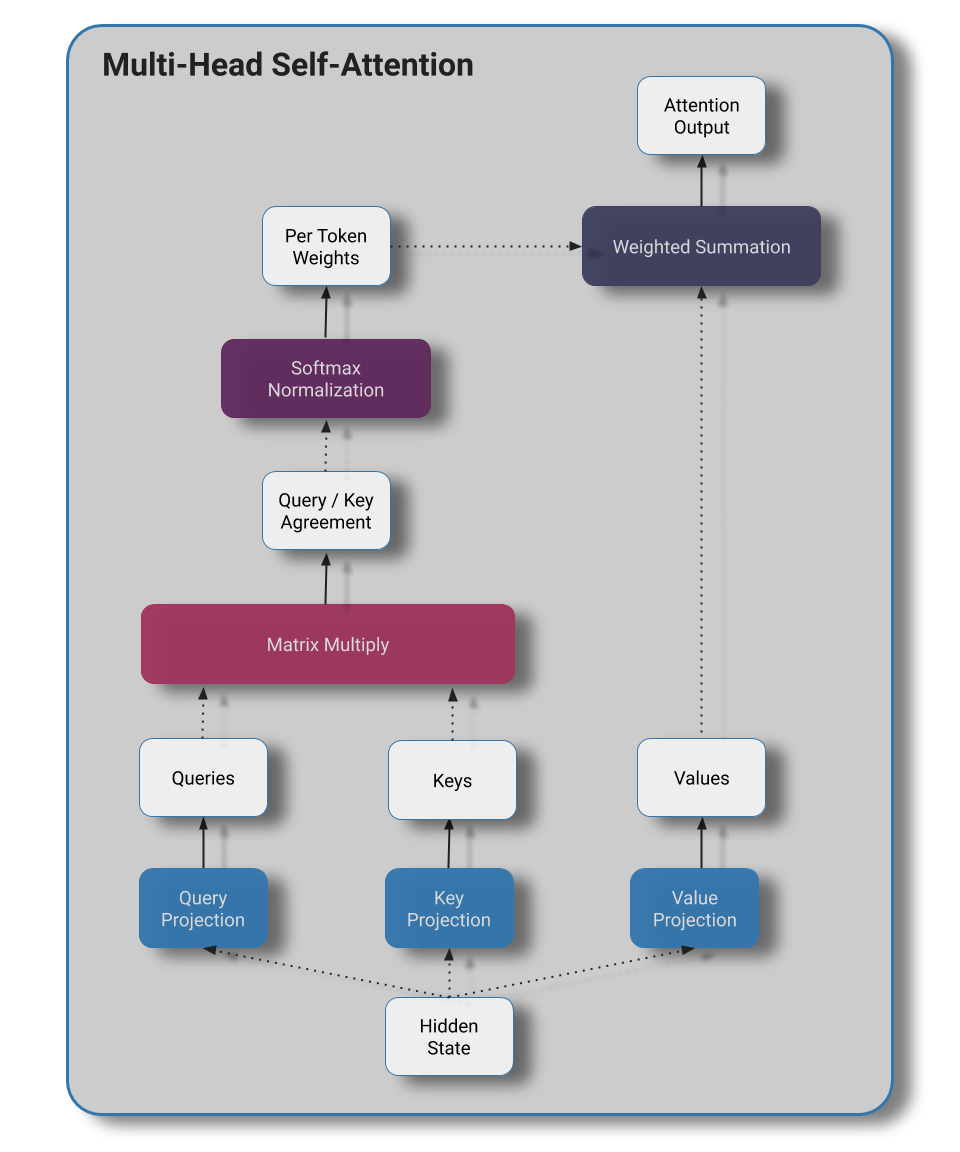
Directions:

Input Attention:

Produce a linear projection from each of the RIM's hidden states, \(h_t\), to act as a query
Project the set of vector valued inputs at that timestep to produce a matrix of keys and values
Compute attention of the RIM hidden states over the set of keys

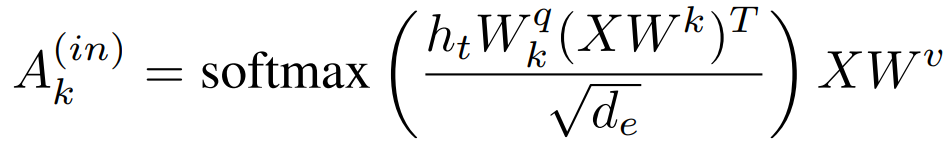
Competition:

Measure each RIM's attention assignment to the zero-vector state. The \(k_A\) RIM's with the smallest attention weights to the null state are considered "active"

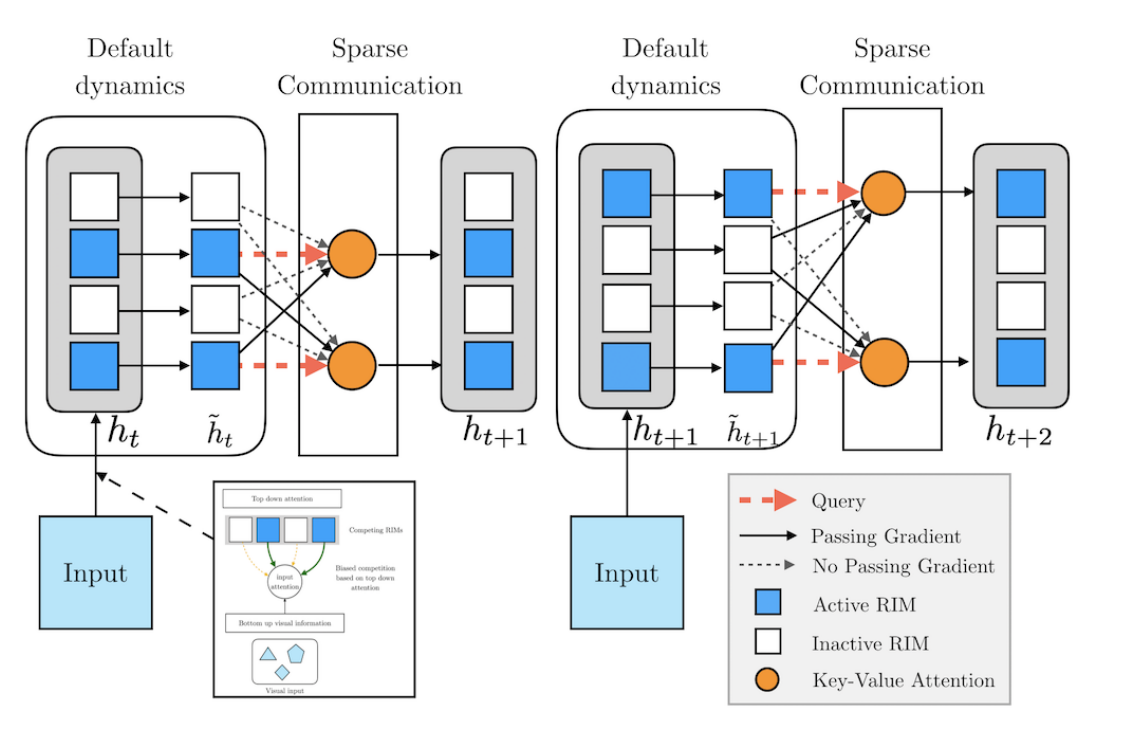
RNN Dynamics:

For active RIMs, apply one LSTM update step, while simply copying inactive RIM state forward.
For each RIM, project the RIM's hidden state at the current timestep to produce a set of keys and values
Compute key-value attention outputs over the set of inputs at the given timestep

Sparse Communication between RIMs:

For active RIMs only, project the hidden state to produce a query
Allow active RIMs to attend over all RIM keys and values and produce their next hidden state via key-value attention with a residual
Disallow backpropagation through the inactive RIMs keys and queries

Visually, our recipe looks like the below:

Figure 1 from "Recurrent Independent Mechanisms"

Experimental Results

The author's of Recurrent Independent Mechanisms elect not to benchmark on standard large-scale sequence modeling tasks of interest and instead focus on probing the generalization properties of the RIMs architecture with simpler tasks.

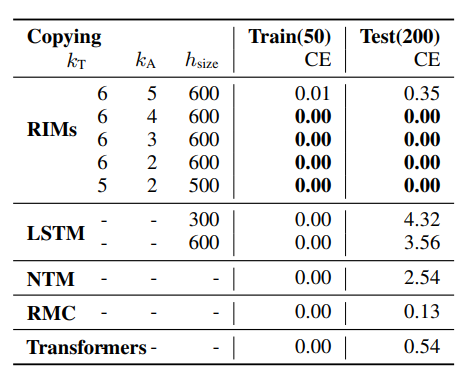
Copying Task:

Models are shown a few characters, then a long run of empty inputs, and are tasked with reproducing the sequence of characters at the beginning of the sequence. When the length of empty inputs is kept constant all standard architectures successfully copy the input sequence, but when the sequence of empty inputs (a distraction) is extended from 50 to 200, all models sans the RIMs architecture fail to generalize.

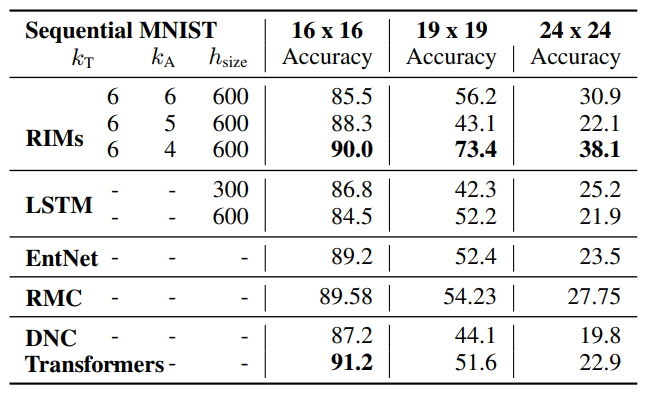
Table 1 from "Recurrent Independent Mechanisms"

Sequential MNIST:

In a related task, the authors perform MNIST digit classification with sequential pixel inputs, then test with larger resolution images. Although the performance of all models degrade, the performance of the RIM architecture degrades most slowly.

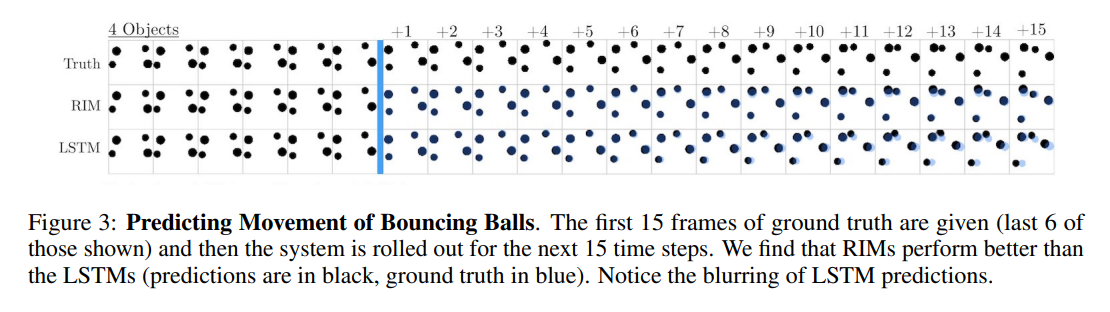
Bouncing Balls

When applied to a task that requires predicting future states of a closed system of bouncing balls, RIMs more closely model the behavior of the simulation than LSTMs and are accurate out to a greater number of timesteps and generalizes more effectively to simulations with a greater number of balls than seen during training.

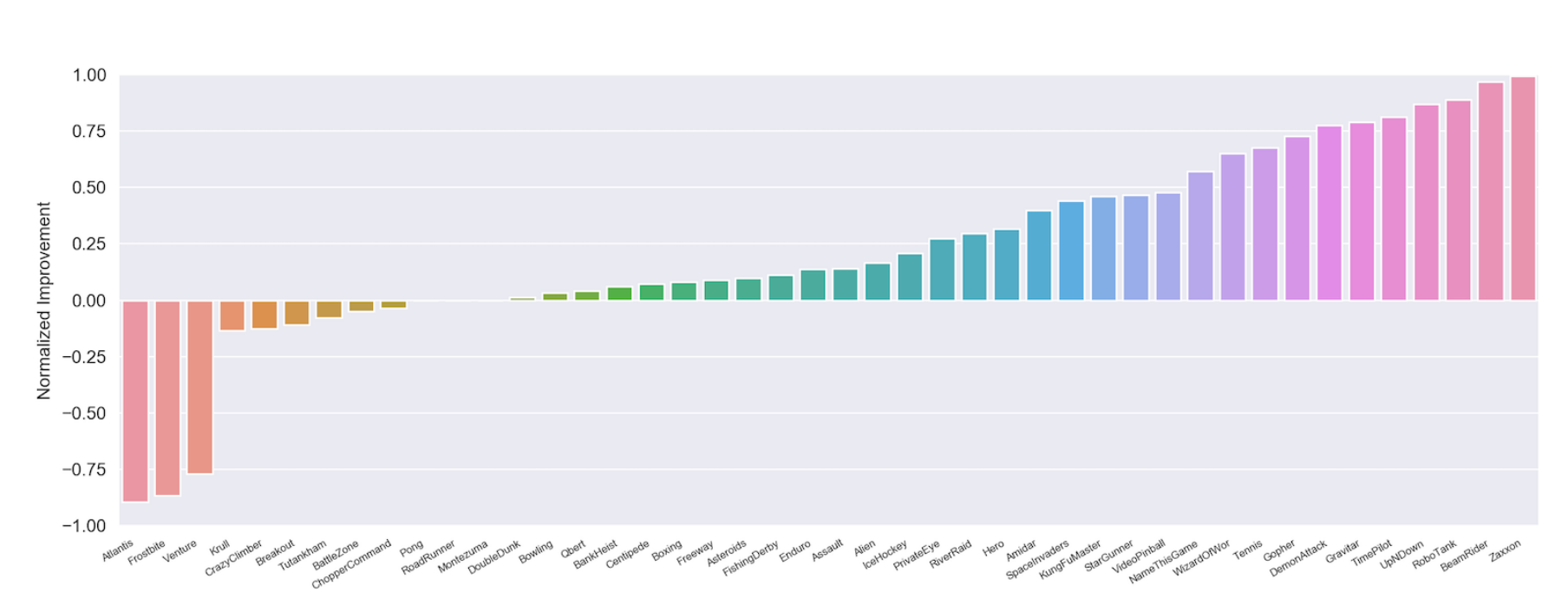
Figure 3 from "Recurrent Independent Mechanisms"

Reinforcement Learning

When Proximal Policy Optimization with RIMs and LSTM policy networks are compared on the full suite of Atari games, RIMs outperform the LSTM baseline on the large majority of tasks.

Figure 6 from "Recurrent Independent Mechanisms"

Extensions

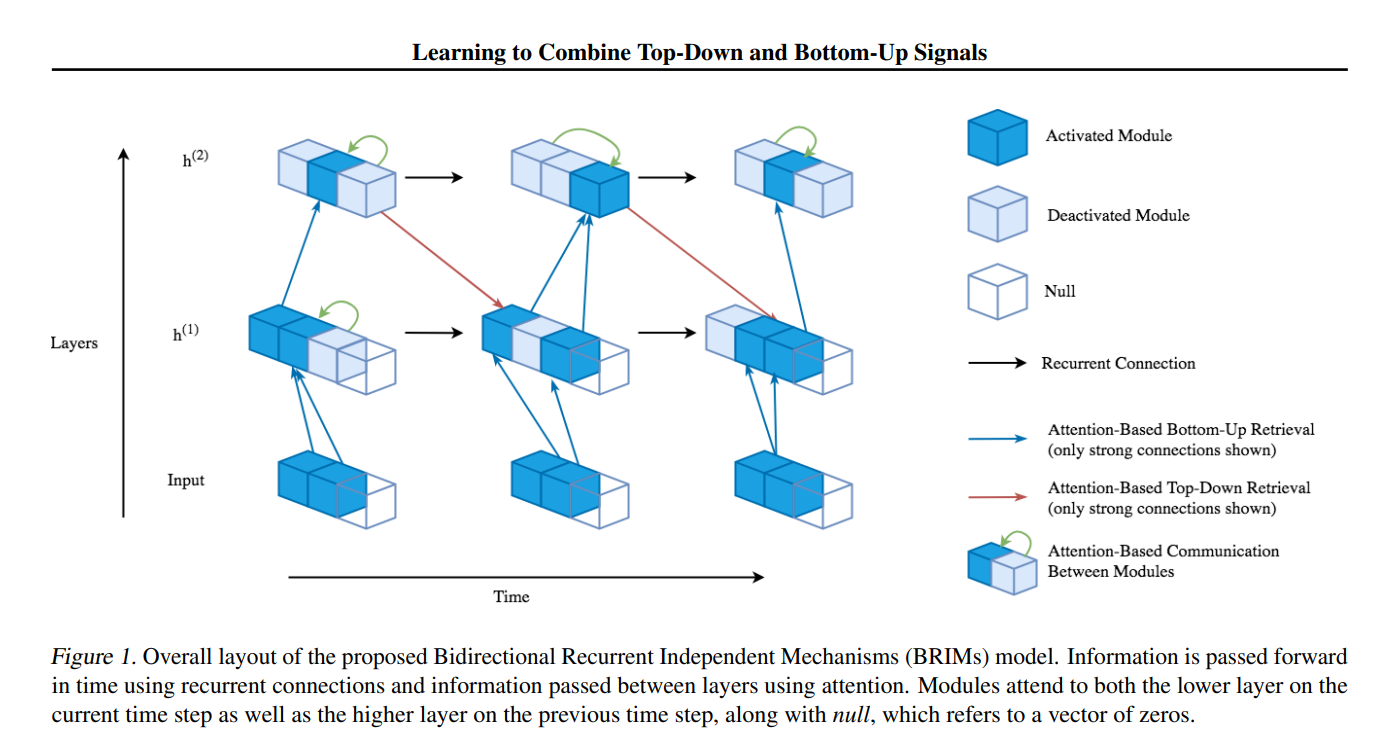
In conjunction with some of the original authors of "Recurrent Independent Mechanisms", Sarthak Mittal built upon the original RIMs work in the paper "Learning to Combine Top-Down and Bottom-Up Signals in Recurrent Neural Networks with Attention over Modules". This work extends RIMs to multiple layers and allows information to flow from higher level layers to lower level layers in a restricted manner.

Like the original RIMs architecture, active mechanisms in each layer attend to all other mechanisms in the same layer. Unlike the original RIMs architecture, each mechanism additionally attends to keys and values from the previous timestep of higher layers and from the current timestep of lower layers.

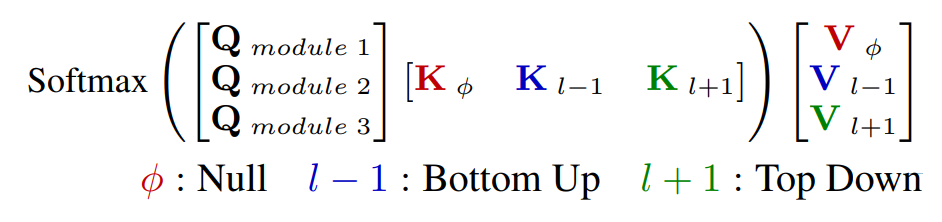
The entire system is illustrated beautifully by the author's diagram below:

Figure 1 from "Learning to Combine Top-Down and Bottom-Up Signals in Recurrent Neural Networks with Attention over Modules"

When tested on the same generalization benchmarks, Mittal et. al found that the addition of the multi-layer structure aids test-time generalization on the same benchmarks used by the original RIMs paper:

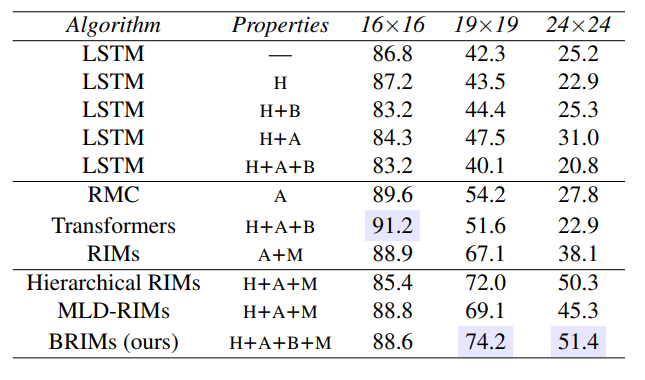
Table 1. Performance on the Sequential MNIST task compared to vanilla RIMs

Also unlike the original RIMs paper, "Learning to Combine Top-Down and Bottom-Up Signals..." additionally benchmarks on the WikiText-103 language modeling benchmark. Although the results lag substantially behind that of modern monolithic transformers, a test score of ~36 PPL is still impressive given that their hyperparameter count is likely well below the 100M+ parameters of the small versions of the transformer family.

Conclusions:

What I appreciated most about this paper is that it forms a hypothesis about what behaviors are desirable for better generalization and designs a novel architecture around this set of desiderata. The concept of top-down attention resonates with me and I do think we could stand to benefit from incorporate this variety of top-down prior into other architectures. I believe that more compartmentalized, modular model architectures such as RIMs have a chance to eventually overturn the current trend towards large densely connected networks with no explicit encouragement of sparsity, and am sincerely looking forward to future work by Anirudh Goyal, Alex Lamb, Sarthak Mittal and co-authors.