Just last month DeepMind open-sourced Haiku, the JAX version of their tensorflow neural network library Sonnet. Today we'll be walking through a port of the RoBERTa pre-trained model to JAX + Haiku, then finetuning the model to solve a downstream task!
If you're unfamiliar with JAX, need a primer on JAX fundamentals, or simply want to know why you should care, check out my previous post -- A First Look at JAX or wander on over to the official JAX documentation.
Some brief notes about the format of this blog post:
- This post will be code-oriented and will usually show code examples first before providing commentary.
- We're going to be working in a top-down fashion, so we'll lay out our Transformer model in broad strokes and then fill in the detail.
- I'll introducing Haiku's features as they're needed for our Transformer finetuning project.
If you'd like to run the code as you read along I've also made this walkthrough available as a Colab notebook.
Without further ado, let's explore Haiku!
DeepMind's Haiku Library
The Haiku README provides an excellent short description of Haiku's role in the JAX ecosystem:
- Haiku is a simple neural network library for JAX that enables users to use familiar object-oriented programming models while allowing full access to JAX's pure function transformations.
- Haiku provides two core tools: a module abstraction, hk.Module, and a simple function transformation, hk.transform.
- hk.Modules are Python objects that hold references to their own parameters, other modules, and methods that apply functions on user inputs.
- hk.transform turns functions that use these object-oriented, functionally "impure" modules into pure functions that can be used with jax.jit, jax.grad, jax.pmap, etc.
In addition to those two key abstractions, Haiku provides a collection of common neural network components like convolutions, pooling operations, RNN / GRU / LSTM units, batch norm and other normalization methods, padding operations, and a suite of a initializers.
Writing Haiku Modules
At the most abstract level, our Haiku Transformer implementation will look like this:
import haiku as hk
class Transformer(hk.Module):
def __init__(self, config, *args, **kwargs):
super().__init__(name="Transformer")
self.config = config
def __call__(self, token_ids):
x = Embedding(config)(token_ids)
for layer_num, layer in enumerate(range(config.n_layers)):
x = TransformerBlock(config, layer_num=layer_num)(x)
return x
First, a comment on how Haiku modules are typically structured. The __init__ function is where we manage module configuration -- storing values like the number of layers in our transformer, our hidden dimension size, and other parameters. In order for Haiku to function properly, the __init__() of all hk.Modules must call super().__init__(), optionally with a name.
Note that if we wanted we could have moved some of this logic around, constructing our TokenEmbedding object in the __init__ method for instance. Although nothing prevents us from doing this, there are times when we don't have enough information to construct all our modules in the __init__ method, often because our configuration is dependent on some property of our input (like the max length of the sequence, or the batch size, or whether dropout should be applied). Because of this, lower level hk.Modules are often constructed in the same method that is called when the module is applied to an input (in our case, __call__). It's also simply convenient to have the full declaration of module settings in line with the application of the module to an input, to prevent hopping back and forth between methods when reading code.
In our example above, we use the __call__ method as our application method for brevity but we could equivalently use forward or any other method name. An hk.Module can also expose more than one application method if desirable.
import haiku as hk
class AlternateTransformer(hk.Module):
"""
An equally valid implementation
"""
def __init__(self, config, *args, **kwargs):
super().__init__(name="Transformer")
self.config = config
self.embedder = Embedding(config)
def embed(self, tokens):
return self.embedder(tokens)
def forward(self, tokens):
x = self.embedder(tokens)
for layer in config.n_layers:
x = TransformerBlock(config)(x)
return x
If we had already implemented the Embedding and TransformerBlock modules, we could convert our new hk.Module to a JAX compatible function through the use of hk.transform.
# We'll fill our our config later
config = {'max_length': 512}
def features(tokens):
transformer = Transformer(config)
return transformer(tokens)
features_fn = hk.transform(features)
Neat! Let's write our Embedding module and plug in some pre-trained model weights so we can start executing code.
Word Embeddings and Positional Embeddings
from transformers import RobertaModel
import jax.numpy as jnp
class Embedding(hk.Module):
"""
Embeds tokens and positions into an array of shape:
[n_batch, n_seq, n_hidden]
"""
def __init__(self, config):
super().__init__()
self.config = config
def __call__(self, token_ids, training=False):
"""
token_ids: ints of shape (batch, n_seq)
"""
word_embeddings = self.config['pretrained'][
'embeddings/word_embeddings'
]
# We have to flatten our tokens before passing them to the
# hk.Embed module, as arrays with more than one dimension
# are interpreted as multi-dimensional indexes
flat_token_ids = jnp.reshape(
token_ids, [token_ids.shape[0] * token_ids.shape[1]]
)
flat_token_embeddings = hk.Embed(
vocab_size=word_embeddings.shape[0],
embed_dim=word_embeddings.shape[1],
# Here we're using hk.initializers.Constant to supply
# pre-trained embeddings to our hk.Embed module
w_init=hk.initializers.Constant(
self.config['pretrained']['embeddings/word_embeddings']
)
)(flat_token_ids)
# After we've embedded our token IDs,
# we reshape to recover our batch dimension
token_embeddings = jnp.reshape(
flat_token_embeddings,
[
token_ids.shape[0],
token_ids.shape[1],
word_embeddings.shape[1]
]
)
# Combine our token embeddings with
# a set of learned positional embeddings
embeddings = (
token_embeddings + PositionEmbeddings(self.config)()
)
embeddings = hk.LayerNorm(
axis=-1,
create_scale=True,
create_offset=True,
# The layer norm parameters are also pretrained,
# so we have to take care to use a constant initializer
# for these as well
scale_init=hk.initializers.Constant(
self.config['pretrained']['embeddings/LayerNorm/gamma']
),
offset_init=hk.initializers.Constant(
self.config['pretrained']['embeddings/LayerNorm/beta']
)
)(embeddings)
# Dropout is will be applied later when we finetune our
# Roberta implementation to solve a classification task.
# For now we'll set `training` to False.
if training:
embeddings = hk.dropout(
# Haiku magic:
# We'll explicitly provide a RNG key to haiku later
# to make this function
hk.next_rng_key(),
rate=self.config['embed_dropout_rate'],
x=embeddings
)
return embeddings
Although it might appear a bit verbose thanks to a half-dozen comments and my foolhardy attempt to keep text from wrapping in the blog's code widget, don't let your eyes glaze over yet. Our Embedding module is relatively straightforward underneath the hood:
- Using
hk.Embed, we perform a lookup to get the vector that corresponds to each of our token IDs. - We initialize this to the pre-trained embedding matrix we downloaded.
- We add
PositionEmbeddings()-- ahk.Modulewe have yet to define. Assuming a fixed sequence length, this is nothing more than a static matrix that we broadcast to each sequence in our batch. - We normalize our embeddings using layer norm, applying the scales and offsets learned during pre-training.
- Finally, we optionally apply dropout to our embeddings at train time.
- Note the
hk.next_rng_key()feature. With vanilla JAX, we would have to make sure to pass ourPRNGKeyaround to every module that needs it. A handy feature of Haiku is that yourPRNGKeyis exposed via thehk.next_rng_keyutility with the context ofhk.transform.
class PositionEmbeddings(hk.Module):
"""
A position embedding of shape [n_seq, n_hidden]
"""
def __init__(self, config):
super().__init__()
self.config = config
# For unknown reasons the Roberta position embeddings are
# offset in the position embedding matrix
self.offset = 2
def __call__(self):
pretrained_position_embedding = self.config['pretrained'][
'embeddings/position_embeddings'
]
position_weights = hk.get_parameter(
"position_embeddings",
pretrained_position_embedding.shape,
init=hk.initializers.Constant(pretrained_position_embedding)
)
start = self.offset
end = self.offset + self.config['max_length']
return position_weights[start:end]
The PositionEmbeddings module is also pretty straightforward -- we simply slice the pre-trained position embedding matrix to the desired length and return it. However, our PositionEmbeddings module has introduced a new key haiku function!
hk.get_parameter(name, shape, dtype, init)
The hk.get_parameter function is how Haiku keeps track of parameter state for us. The module we're in and the name argument passed to hk.get_parameter serve as keys to register this new parameter in a Haiku-managed parameter store. If we were writing something similar with vanilla JAX, we would have to keep track of these parameters manually. Later on we'll see how hk.transform allows us to retrieve the values of our parameters using init().
Extended docs for hk.get_parameter are available in the official Haiku documentation.
Pretrained Weights and Tokenization
Now that you're familiar with hk.get_parameter, let's load in some pre-trained model weights so we can test out what we've put together so far.
from io import BytesIO
from functools import lru_cache
import joblib
import requests
from transformers import RobertaModel, RobertaTokenizer
# We'll use these later as a means to check our implementation
huggingface_roberta = RobertaModel.from_pretrained(
'roberta-base', output_hidden_states=True
)
huggingface_tokenizer = RobertaTokenizer.from_pretrained('roberta-base')
# Some light postprocessing to make parameter keys more concise
def postprocess_key(key):
key = key.replace('model/featurizer/bert/', '')
key = key.replace(':0', '')
key = key.replace('self/', '')
return key
# Cache the downloaded file to go easy on the tubes
@lru_cache()
def get_pretrained_weights():
# We'll use the weight dictionary from the Roberta encoder at
# https://github.com/IndicoDataSolutions/finetune
remote_url = "https://bendropbox.s3.amazonaws.com/roberta/roberta-model-sm-v2.jl"
weights = joblib.load(BytesIO(requests.get(remote_url).content))
weights = {
postprocess_key(key): value
for key, value in weights.items()
}
# We use huggingface's word embedding matrix because their token ID
# mapping varies slightly from the format in the joblib file above
input_embeddings = huggingface_roberta.get_input_embeddings()
weights['embeddings/word_embeddings'] = (
input_embeddings.weight.detach().numpy()
)
return weights
class Scope(object):
"""
A tiny utility to help make looking up into our dictionary cleaner.
There's no haiku magic here.
"""
def __init__(self, weights, prefix):
self.weights = weights
self.prefix = prefix
def __getitem__(self, key):
return self.weights[self.prefix + key]
pretrained = get_pretrained_weights()
print([k for k in pretrained.keys() if 'embedding' in k])
['embeddings/word_embeddings', 'embeddings/LayerNorm/beta', 'embeddings/LayerNorm/gamma', 'embeddings/token_type_embeddings', 'embeddings/position_embeddings']
Looks like we have the weights we need for our Embedding module, but we're still missing a way to go from text to numeric token IDs in our word embedding matrix. Let's load in the pre-written tokenizer from huggingface to save ourselves some pain, because the only thing more painful than writing tokenizer code is reading about someone writing tokenizer code.
sample_text = """
This was a lot less painful than re-implementing a tokenizer
"""
encoded = huggingface_tokenizer.batch_encode_plus(
[sample_text, sample_text],
pad_to_max_length=True,
max_length=config['max_length']
)
sample_tokens = encoded['input_ids']
print(sample_tokens[0][:20])
[0, 152, 21, 10, 319, 540, 8661, 87, 769, 12, 757, 40224, 154, 10, 19233, 6315, 2, 1, 1, 1]
Looks good! We've passed the pad_to_max_length and max_length arguments so that the huggingface_tokenizer can handle padding out sequences to a constant length for us -- and it's working as the trailing 1's above show us. Token ID 1 corresponds to the padding token used by RoBERTa.
Running our Embedding Module
Now we have all the necessary ingredients to test out our embedding layer, let's hk.transform the embedding operation and take things for a spin.
from jax import jit
from jax.random import PRNGKey
import numpy as np
config = {
'pretrained': pretrained,
'max_length': 512,
'embed_dropout_rate': 0.1
}
def embed_fn(tokens, training=False):
embedding = Embedding(config)(tokens)
return embedding
rng = PRNGKey(42)
embed = hk.transform(embed_fn, apply_rng=True)
sample_tokens = np.asarray(sample_tokens)
params = embed.init(rng, sample_tokens, training=False)
embedded_tokens = embed.apply(params, rng, sample_tokens)
print(embedded_tokens.shape)
(2, 512, 768)
With that, we've successfully executed our first snippet of code using Haiku!
In the code above, we first wrote embed_fn to instantiate an instance of our Embedding module and call it. This is necessary to wrap up all the requisite state for the embedding function for haiku.
If you accidentally try to instantiate a hk.Module outside of a hk.transform context you'll receive a helpful reminder that this isn't permitted. Haiku imposes this constraint so it can "purify" our stateful hk.Module and convert it into a pure function that functions with JAX.
embedding = Embedding(config)
ValueError: All `hk.Module`s must be initialized inside an `hk.transform`.
You've probably also noticed that we're using two methods we haven't yet spoken about -- init() and apply().
params = embed.init(rng, sample_tokens, training=False)
The init method is a haiku utility that gathers up all the parameters of our custom haiku modules for us and consolidates them into a frozendict. The init() method is also responsible for initializing any unitialized parameters, which is why we pass a source of randomness (our rng) as the first argument.
Let's inspect our params variable:
print({key: type(value) for key, value in params.items()})
{'embedding/embed': haiku._src.data_structures.frozendict, 'embedding/layer_norm': haiku._src.data_structures.frozendict, 'embedding/position_embeddings': haiku._src.data_structures.frozendict}
When we use a hk.Module within another hk.Module, it gets placed in a subdictionary. But if we drill down into our frozendict we'll eventually hit the bottom and uncover an np.ndarray -- the current state of the weights of our model. If you're familiar with tensorflow's concept of a variable scope, this should feel familiar.
print({key: type(value) for key, value in params['embedding/layer_norm'].items()})
{'offset': <class 'numpy.ndarray'>, 'scale': <class 'numpy.ndarray'>}
It's worth noting, however, that we need to use haiku's hk.get_parameter construct (or a hk.Module) for the parameters to be tracked automatically. If we try to use a simple jnp.ndarray within the context of hk.transform it won't be tracked as a trainable parameter.
import numpy as np
import jax
def linear_fn(x):
w = jax.random.normal(hk.next_rng_key(), (10, 10))
b = jnp.zeros(10)
return np.dot(w, x) + b
linear = hk.transform(linear_fn)
params = linear.init(PRNGKey(0), np.random.rand(10))
print(params.keys())
KeysOnlyKeysView([])
The second new method is .apply():
embedded_tokens = embed.apply(params, rng, sample_tokens)
The apply() method injects the parameters of our model (and if we've passed apply_rng to hk.transform, our pseudo-random number generator) to the embed function so that we have all the necessary state to compute the output of our function. This pattern is how hk.transform is able to turn a stateful hk.Module class into a JAX compatible operation -- init() and apply() are natural counterparts. Our init() method extracts the problematic state from our module, and the second passes that state back into the pure apply() method. Because apply() is functionally pure, we're totally free to compose it with any of the standard JAX operations like jit() and grad()!
embedded_tokens = jit(embed.apply)(params, rng, sample_tokens)
In all honestly, that's about all there is to working with Haiku! That's part of the beauty of it -- Haiku aims to be a library, not a framework -- providing a suite of utilities that complement JAX but doing it's best not to get in your way by requiring custom formats or imposing problematic constraints.
If you're interested in more detail on how hk.Module and hk.transform function, I'd recommend Sabrina Mielke's recent article, "From PyTorch to JAX: towards neural net frameworks that purify stateful code", which builds up the motivation for the design decisions that Haiku made.
A Transformer Block Module
With the critical pieces of the haiku API behind us, let's continue implementing our transformer! Next up -- the TransformerBlock module.

class TransformerBlock(hk.Module):
def __init__(self, config, layer_num):
super().__init__()
self.config = config
self.n = layer_num
def __call__(self, x, mask, training=False):
scope = Scope(
self.config['pretrained'], f'encoder/layer_{self.n}/'
)
# Feed our input through a multi-head attention operation
attention_output = MultiHeadAttention(
self.config, self.n
)(x, mask, training=training)
# Add a residual connection with the input to the layer
residual = attention_output + x
# Apply layer norm to the combined output
attention_output = hk.LayerNorm(
axis=-1,
create_scale=True,
create_offset=True,
scale_init=hk.initializers.Constant(
scope['attention/output/LayerNorm/gamma']
),
offset_init=hk.initializers.Constant(
scope['attention/output/LayerNorm/beta']
),
)(residual)
# Project out to a larger dim, apply a gelu,
# and then project back down to our hidden dim
mlp_output = TransformerMLP(
self.config, self.n
)(attention_output, training=training)
# Residual connection to the output of the attention operation
output_residual = mlp_output + attention_output
# Apply another LayerNorm
layer_output = hk.LayerNorm(
axis=-1,
create_scale=True,
create_offset=True,
scale_init=hk.initializers.Constant(
scope['output/LayerNorm/gamma']
),
offset_init=hk.initializers.Constant(
scope['output/LayerNorm/beta']
),
)(output_residual)
return layer_output
At this level of abstraction the flow is still fairly simple. We feed the inputs to each transformer block through it's signature self-attention layer, then add in residuals and apply layer normalization.
We then feed the attention outputs through a 2 layer MLP, apply the residuals from the self-attention output, and apply a second layer normalization step.
Multi-Head Self-Attention
Let's define our MultiHeadAttention layer next.
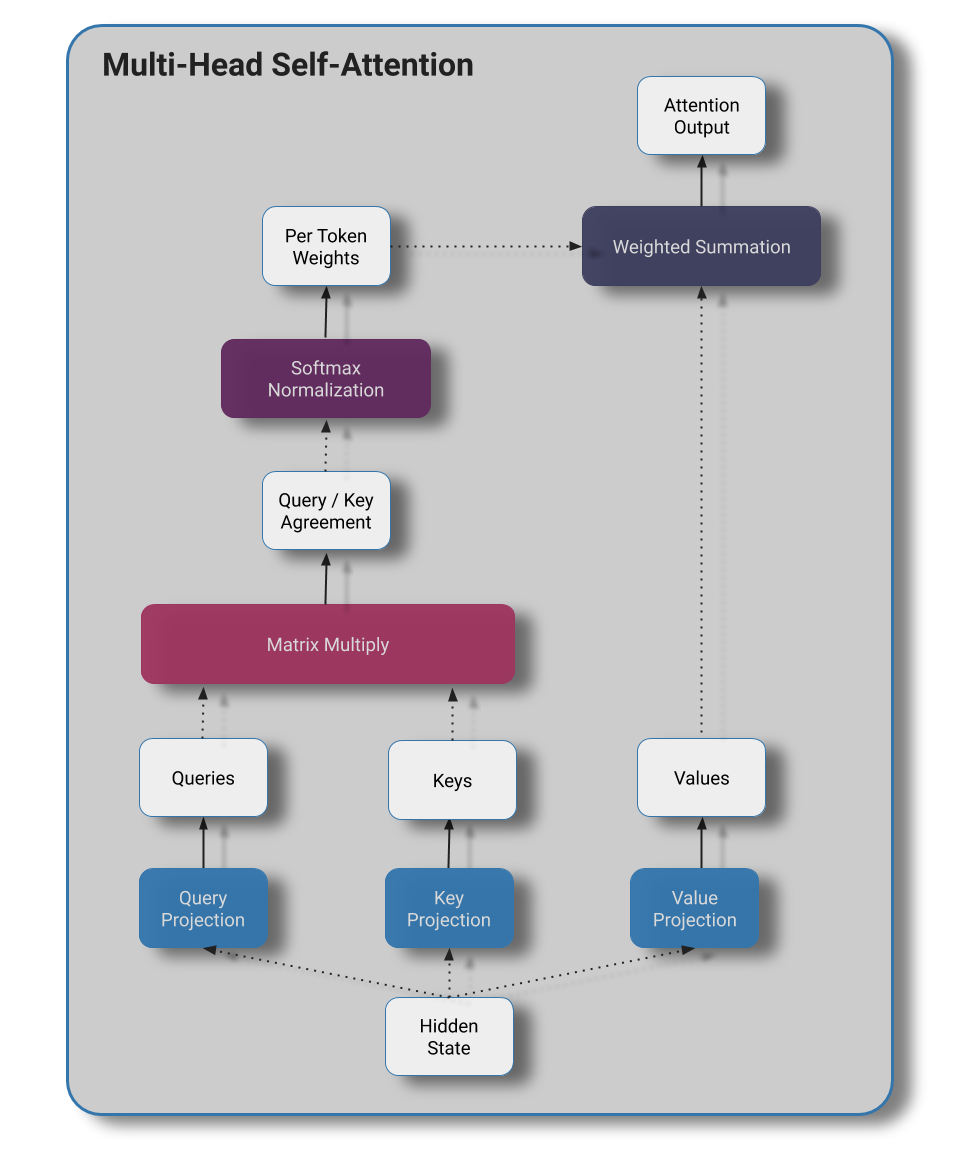
class MultiHeadAttention(hk.Module):
def __init__(self, config, layer_num):
super().__init__()
self.config = config
self.n = layer_num
def _split_into_heads(self, x):
return jnp.reshape(
x,
[
x.shape[0],
x.shape[1],
self.config['n_heads'],
x.shape[2] // self.config['n_heads']
]
)
def __call__(self, x, mask, training=False):
"""
x: tensor of shape (batch, seq, n_hidden)
mask: tensor of shape (batch, seq)
"""
scope = Scope(self.config['pretrained'], f'encoder/layer_{self.n}/attention/')
# Project to queries, keys, and values
# Shapes are all [batch, sequence_length, hidden_size]
queries = hk.Linear(
output_size=self.config['hidden_size'],
w_init=hk.initializers.Constant(scope['query/kernel']),
b_init=hk.initializers.Constant(scope['query/bias'])
)(x)
keys = hk.Linear(
output_size=self.config['hidden_size'],
w_init=hk.initializers.Constant(scope['key/kernel']),
b_init=hk.initializers.Constant(scope['key/bias'])
)(x)
values = hk.Linear(
output_size=self.config['hidden_size'],
w_init=hk.initializers.Constant(scope['value/kernel']),
b_init=hk.initializers.Constant(scope['value/bias'])
)(x)
# Reshape our hidden state to group into heads
# New shapes are:
# [batch, sequence_length, n_heads, size_per_head]
queries = self._split_into_heads(queries)
keys = self._split_into_heads(keys)
values = self._split_into_heads(values)
# Compute per head attention weights
# b: batch
# s: source sequence
# t: target sequence
# n: number of heads
# h: per-head hidden state
# Note -- we could also write this with jnp.reshape
# and jnp.matmul, but I'm becoming a fan of how concise
# opting to use einsum notation for this kind of operation is.
# For more info, see:
# https://rockt.github.io/2018/04/30/einsum or
# any of Noam Shazeer's recent Transformer papers
attention_logits = jnp.einsum('bsnh,btnh->bnst', queries, keys)
attention_logits /= np.sqrt(queries.shape[-1])
# Add logits of mask tokens with a large negative number
# to prevent attending to those terms.
attention_logits += jnp.reshape(
mask * -2**32, [mask.shape[0], 1, 1, mask.shape[1]]
)
attention_weights = jax.nn.softmax(attention_logits, axis=-1)
per_head_attention_output = jnp.einsum(
'btnh,bnst->bsnh', values, attention_weights
)
attention_output = jnp.reshape(
per_head_attention_output,
[
per_head_attention_output.shape[0],
per_head_attention_output.shape[1],
per_head_attention_output.shape[2] *
per_head_attention_output.shape[3]
]
)
# Apply dense layer to output of attention operation
attention_output = hk.Linear(
output_size=self.config['hidden_size'],
w_init=hk.initializers.Constant(
scope['output/dense/kernel']
),
b_init=hk.initializers.Constant(
scope['output/dense/bias']
)
)(attention_output)
# Apply dropout at training time
if training:
attention_output = hk.dropout(
rng=hk.next_rng_key(),
rate=self.config['attention_drop_rate'],
x=attention_output
)
return attention_output
- We project our hidden state out to key, query, and value tensors of the same dimensions as the input hidden state
- We then reshape the last dimension of our matrix to group neighboring activations into N heads
- Queries and keys are dotted to produce a measure of agreement that we'll use as an attention logit
- We divide by the sequence length to soften our attention distribution
- We apply our softmax to produce our attention weights that sum to 1.
- We then use our attention weights in conjunction with our values to produce our new hidden state
- We reshape our matrices to re-combine the heads.
- Finally, we apply a linear projection to our attention outputs and optionally apply dropout at training time.
We won't spent too much time on the details here, as the intent of this blog post is to highlight using JAX and Haiku rather than devote too much time to an explanation of self-attention.
If you'd like a more in-depth refresher on the self-attention operation, I'd recommend:
Transformer MLP

def gelu(x):
"""
We use this in place of jax.nn.relu because the approximation used
produces a non-trivial difference in the output state
"""
return x * 0.5 * (1.0 + jax.scipy.special.erf(x / jnp.sqrt(2.0)))
class TransformerMLP(hk.Module):
def __init__(self, config, layer_num):
super().__init__()
self.config = config
self.n = layer_num
def __call__(self, x, training=False):
# Project out to higher dim
scope = Scope(
self.config['pretrained'], f'encoder/layer_{self.n}/'
)
intermediate_output = hk.Linear(
output_size=self.config['intermediate_size'],
w_init=hk.initializers.Constant(
scope['intermediate/dense/kernel']
),
b_init=hk.initializers.Constant(
scope['intermediate/dense/bias']
)
)(x)
# Apply gelu nonlinearity
intermediate_output = gelu(intermediate_output)
# Project back down to hidden size
output = hk.Linear(
output_size=self.config['hidden_size'],
w_init=hk.initializers.Constant(
scope['output/dense/kernel']
),
b_init=hk.initializers.Constant(
scope['output/dense/bias']
),
)(intermediate_output)
# Apply dropout at training time
if training:
output = hk.dropout(
rng=hk.next_rng_key(),
rate=self.config['fully_connected_drop_rate'],
x=output
)
return output
The final component of our pre-trained RoBERTa model is the Transformer MLP block. The MLP block contains:
- A linear up-projection from our hidden size to a larger intermediate hidden representation
- The application of a single gaussian error linear unit (GELU)
- A linear projection back down to our hidden size
As per usual, we optionally apply dropout at training time.
Tying it All Together – Roberta Featurizer
In the code block below, we wrap up all our previous work, embedding our input token IDs with our Embedding module and applying 12 layers of our TransformerBlock.
import haiku as hk
class RobertaFeaturizer(hk.Module):
def __init__(self, config, *args, **kwargs):
super().__init__(name="Transformer")
self.config = config
def __call__(self, token_ids, training=False):
x = Embedding(self.config)(token_ids, training=training)
mask = (token_ids == self.config['mask_id']).astype(jnp.float32)
for layer_num, layer in enumerate(range(config['n_layers'])):
x = TransformerBlock(
config, layer_num=layer_num
)(x, mask, training=training)
return x
With that final hk.Module complete, we'll populate the config object we've been referencing through our hk.Module's and apply hk.transform to produce a pure function. Even without attaching a classification head to the pre-trained base, we already have features we could use for purposes of computing textual similarities or similar.
from jax import jit
from jax.random import PRNGKey
config = {
'pretrained': pretrained,
'max_length': 512,
'embed_dropout_rate': 0.1,
'fully_connected_drop_rate': 0.1,
'attention_drop_rate': 0.1,
'hidden_size': 768,
'intermediate_size': 3072,
'n_heads': 12,
'n_layers': 12,
'mask_id': 1,
'weight_stddev': 0.02,
# For use later in finetuning
'n_classes': 2,
'classifier_drop_rate': 0.1,
'learning_rate': 1e-5,
'max_grad_norm': 1.0,
'l2': 0.1,
'n_epochs': 5,
'batch_size': 4
}
def featurizer_fn(tokens, training=False):
contextual_embeddings = RobertaFeaturizer(config)(
tokens, training=training
)
return contextual_embeddings
rng = PRNGKey(42)
roberta = hk.transform(featurizer_fn, apply_rng=True)
sample_tokens = np.asarray(sample_tokens)
params = roberta.init(rng, sample_tokens, training=False)
contextual_embedding = jit(roberta.apply)(params, rng, sample_tokens)
print(contextual_embedding.shape)
(2, 512, 768)
Sanity Checks and Debugging JAX
Let's check to make sure our implementation matches up with a known functional implementation -- we'll opt to use the hugging face model we instantiated earlier.
import torch
batch_token_ids = torch.tensor(huggingface_tokenizer.encode(sample_text)).unsqueeze(0)
huggingface_output_state, huggingface_pooled_state, _ = huggingface_roberta.forward(batch_token_ids)
print(np.allclose(
huggingface_output_state.detach().numpy(),
contextual_embedding[:1, :batch_token_ids.size()[1]],
atol=1e-3
))
True
Great! The contextual embeddings line up, so our implementation is correct.
Admittedly, the first time I ran this things didn't go quite so smoothly -- I missed the subtle difference in the two gelu implementations and the difference in outputs was enough to make this check fail. We can't directly inspect the intermediate outputs of our functions if we have things wrapped in a jit call like our example above, but if you remove the jit call to roberta.apply, we can add vanilla Python print statements to our implementation to track activations at intermediate points in our network and compare to the Hugging Face implementation. This is a common gotcha if you're new to JAX, and I recommend reading JAX core developer Matthew Johnson's response to a github issue on the topic of printing within jit if you're curious why this limitation exists.
Finetuning for Classification
Now that our featurizer is implemented, let's wrap this up to use for downstream classification tasks!
This is as easy as slicing off the hidden state of the first token and applying a linear projection.
class RobertaClassifier(hk.Module):
def __init__(self, config, *args, **kwargs):
super().__init__(name="Transformer")
self.config = config
def __call__(self, token_ids, training=False):
sequence_features = RobertaFeaturizer(self.config)(
token_ids=token_ids, training=training
)
# Our classifier representation is just the
# output state of our first token
clf_state = sequence_features[:,0,:]
if training:
clf_state = hk.dropout(
rng=hk.next_rng_key(),
rate=self.config['classifier_drop_rate'],
x=clf_state
)
# We project down from our hidden dimension
# to n_classes and use this as our softmax logits
clf_logits = hk.Linear(
output_size=self.config['n_classes'],
w_init=hk.initializers.TruncatedNormal(
self.config['weight_stddev']
)
)(clf_state)
return clf_logits
Data
Let's plug in a real dataset to try it out. As much as I dislike the trope of testing text classifiers on sentiment analysis, we'll be using the IMDB Sentiment dataset from tensorflow datasets because it's already packaged up neatly for us.
import tensorflow_datasets as tfds
def load_dataset(
split,
training,
batch_size,
n_epochs=1,
n_examples=None
):
"""Loads the dataset as a generator of batches."""
ds = tfds.load(
"imdb_reviews",
split=f"{split}[:{n_examples}]"
).cache().repeat(n_epochs)
if training:
ds = ds.shuffle(10 * batch_size, seed=0)
ds = ds.batch(batch_size)
return tfds.as_numpy(ds)
n_examples = 25000
train = load_dataset("train", training=True, batch_size=4, n_epochs=config['n_epochs'], n_examples=n_examples)
INFO:absl:No config specified, defaulting to first: imdb_reviews/plain_text
INFO:absl:Overwrite dataset info from restored data version.
INFO:absl:Reusing dataset imdb_reviews (/home/m/tensorflow_datasets/imdb_reviews/plain_text/1.0.0)
INFO:absl:Constructing tf.data.Dataset for split train[:25000], from /home/m/tensorflow_datasets/imdb_reviews/plain_text/1.0.0
We'll add in an encode_batch utility to make calling the huggingface tokenizer more concise, transformer our new RobertaClassifier module into a pure function, and initialize our model state.
def encode_batch(batch_text):
# Accept either utf-8 encoded bytes or unicode
batch_text = [
text.decode('utf-8') if isinstance(text, bytes) else text
for text in batch_text
]
# Use huggingface's tokenizer to convert
# from raw text to integer token ids
token_ids = huggingface_tokenizer.batch_encode_plus(
batch_text,
pad_to_max_length=True,
max_length=config['max_length'],
)['input_ids']
return np.asarray(token_ids)
Transform, Init, Apply, and JIT!
We're in the home stretch now. We wrap up our RobertaClassifier in a function so we can purify it with hk.transform – again making sure to pass apply_rng as we're using dropout – and initialize the parameters of our RobertaClassifier model.
from jax.experimental import optix
def roberta_classification_fn(batch_token_ids, training):
model = RobertaClassifier(config)(
jnp.asarray(batch_token_ids),
training=training
)
return model
# Purify our RobertaClassifier through the use of hk.transform
# and initialize our classifier
rng = jax.random.PRNGKey(42)
roberta_classifier = hk.transform(roberta_classification_fn, apply_rng=True)
params = roberta_classifier.init(
rng,
batch_token_ids=encode_batch(['Sample text', 'Sample text']),
training=True
)
Next we jit compile some functions that use our RoBERTa classifier for computing the loss, measuring model accuracy, and computing gradient updates.
The first argument to roberta_classifier.apply is always our params, and since we used apply_rng we also have to pass in an rng argument. After the required haiku arguments we can supply the rest of the arguments our transformed roberta_classifier function expects.
Note that our update function calls our loss function -- so although we didn't decorate our loss function with @jax.jit directly we'll still reap the benefits when we call update.
def loss(params, rng, batch_token_ids, batch_labels):
logits = roberta_classifier.apply(
params, rng, batch_token_ids, training=True
)
labels = hk.one_hot(batch_labels, config['n_classes'])
softmax_xent = -jnp.sum(labels * jax.nn.log_softmax(logits))
softmax_xent /= labels.shape[0]
return softmax_xent
@jax.jit
def accuracy(params, rng, batch_token_ids, batch_labels):
predictions = roberta_classifier.apply(
params, rng, batch_token_ids, training=False
)
return jnp.mean(jnp.argmax(predictions, axis=-1) == batch_labels)
@jax.jit
def update(params, rng, opt_state, batch_token_ids, batch_labels):
batch_loss, grads = jax.value_and_grad(loss)(
params, rng, batch_token_ids, batch_labels
)
updates, opt_state = opt.update(grads, opt_state)
new_params = optix.apply_updates(params, updates)
return new_params, opt_state, batch_loss
Training Loop
Finetuning transformers for downstream tasks requires a few tricks for reliable performance -- we'll use a linear warmup + decay along with gradient clipping for our optimizers. JAX exposes 2 different sets of optimization utilities in jax.experimental.optimizers and jax.experimental.optix respectively. As these packages are marked as experimental, I'm not sure if both will be a portion of the JAX library long term or if the plan is for one to supercede the other.
For finetuning RoBERTa we'll be using the latter, as it includes learning rate schedule utilities through optix.scale_by_schedule as well as a utility for gradient clipping with optix.clip_by_global_norm. We can apply our bag of optimization tricks in combination with a vanilla adam optimizer using optix.chain as shown below.
def make_lr_schedule(warmup_percentage, total_steps):
def lr_schedule(step):
percent_complete = step / total_steps
before_peak = jax.lax.convert_element_type(
(percent_complete <= warmup_percentage),
np.float32
)
scale = (
(
before_peak * (percent_complete / warmup_percentage) +
(1 - before_peak)
) * (1 - percent_complete)
)
return scale
return lr_schedule
total_steps = config['n_epochs'] * (n_examples // config['batch_size'])
lr_schedule = make_lr_schedule(
warmup_percentage=0.1, total_steps=total_steps
)
opt = optix.chain(
optix.clip_by_global_norm(config['max_grad_norm']),
optix.adam(learning_rate=config['learning_rate']),
optix.scale_by_schedule(lr_schedule)
)
opt_state = opt.init(params)
Below, we throw together one final utility before writing our training loop -- a short convenience function to print how our train and test accuracy change over time.
def measure_current_performance(params, n_examples=None, splits=('train', 'test')):
# Load our training evaluation and test evaluation splits
if 'train' in splits:
train_eval = load_dataset("train", training=False, batch_size=25, n_examples=n_examples)
# Compute mean train accuracy
train_accuracy = np.mean([
accuracy(
params,
rng,
encode_batch(train_eval_batch['text']),
train_eval_batch['label']
)
for train_eval_batch in train_eval
])
print(f"\t Train validation acc: {train_accuracy:.3f}")
if 'test' in splits:
test_eval = load_dataset("test", training=False, batch_size=25, n_examples=n_examples)
# Compute mean test accuracy
test_accuracy = np.mean([
accuracy(
params,
rng,
encode_batch(test_eval_batch['text']),
test_eval_batch['label'],
)
for test_eval_batch in test_eval
])
print(f"\t Test validation accuracy: {test_accuracy:.3f}")
Finally, in our training loop, we simply pull batches of examples from our training data iterator and call the update function to modify the state of our parameters.
for step, train_batch in enumerate(train):
if step % 100 == 0:
print(f"[Step {step}]")
if step % 1000 == 0 and step != 0:
measure_current_performance(params, n_examples=100)
# Perform adam update
next_batch = next(train)
batch_token_ids = encode_batch(next_batch['text'])
batch_labels = next_batch['label']
params, opt_state, batch_loss = update(
params, rng, opt_state, batch_token_ids, batch_labels
)
[Step 0]
[Step 100]
[Step 200]
[Step 300]
[Step 400]
[Step 500]
[Step 600]
[Step 700]
[Step 800]
[Step 900]
[Step 1000]
Train acc: 0.950
Test accuracy: 0.870
[Step 1100]
[Step 1200]
[Step 1300]
[Step 1400]
...
[Step 15300]
[Step 15400]
[Step 15500]
[Step 15600]When all is said and done, we achieve a respectable test accuracy of 0.944 on the IMDB review dataset. Not too shabby!
measure_current_performance(params, n_examples=25000, splits='test')
Test accuracy: 0.944I hope this post has been useful for folks interested in using JAX and Haiku for side projects that might be concerned about the smaller community and more sparse documentation. In my experience so far both JAX and Haiku are quite usable in spite of their age relative to Tensorflow and PyTorch. Although a Transformer port isn't the best demonstration of the benefits of using JAX and Haiku, their toolbox is a pleasure to use and think they both stand a chance to see real adoption in years to come.



