In recent years, Transformer-based language models have yielded substantial progress in neural machine translation, natural language inference, and a host of other natural language understanding tasks. Self-supervised pre-training via variants of language modeling losses means models trained on broad corpora can improve downstream performance on a wide range of tasks. However, high parameter counts and a large computational footprint mean production deployment of BERT and friends remains difficult. Thankfully, the past 2 years have seen the development of a diverse variety of techniques to ease the pain and yield faster prediction times. In particular, this post focuses on the following suite of methods applied after base model pre-training to reduce the computational cost of prediction:
- Numeric Precision Reduction: yielding speedups through the use of floating point reduction and quantization
- Operation Fusion: numerical tricks to merge select nodes in computational graphs
- Pruning: identifying and removing non-essential portions of a network
- Knowledge Distillation: efficiently training smaller student models to mimic the behavior of more expressive and expensive teachers
- Module Replacement: reducing model complexity or depth via a replacement curriculum
Numeric Precision Reduction:
Perhaps the most-general method for yielding prediction-time speedups in numeric precision reduction. In past years poor support for float16 operations on GPU hardware meant that reducing the precision of weights and activations was often counter-productive, but the introduction of the NVIDIA Volta and Turing architectures with Tensor Cores means modern GPUs are now well equipped for efficient float16 arithmetic.
Floating Point Representation
Floating point types store numeric information of three types – the sign, exponent, and fraction. Traditional float32 representations have 8 bits and 23 bits respectively to represent the exponent and fraction. Traditional float16 representations (the format used for NVIDIA hardware) roughly halve both the exponent and fraction components of the representation. TPUs use a variant called bfloat16 that opts to shift some bits from the fraction to the exponent, trading some precision for the ability to represent a broader range of values.
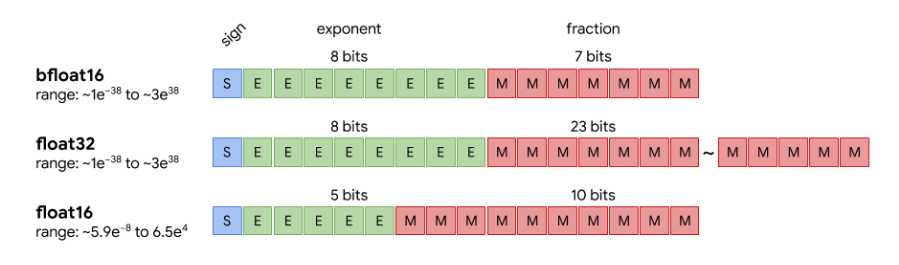
Most of a transformer network can be naively converted to float16 weights and activations with no accuracy penalty. Small portions of the network – in particular, portions of the softmax operation – must remain in float32. This is because the sum of a large number of small values (our logits) can be a source of accumulated error. Because both float16 and float32 values are used, this method is often referred to as "mixed-precision".
Less precise numeric representations enable speedups from two sources.
- Native half-precision instructions
- Larger batch sizes thanks to more compact representations
NVIDIA has published a rather extensive suite of benchmarks relating to floating point precision reduction – in practice this method yields speedups up to 3x.
Integer Quantization
Quantization of float32 to int8 values is also possible but requires more nuanced application. In particular, a post-training calibration step is necessary to ensure that the int8 comptutation is as close as possible to computation performed with float32 values.
If you know what range of values a network's activations will likely occupy, you can divide up that range into 256 discrete chunks and assign each to an integer. As long as you store the the scale factor and the range occupied, you can use the integer approximations for your matrix multiplies and recover a floating point value at the output.
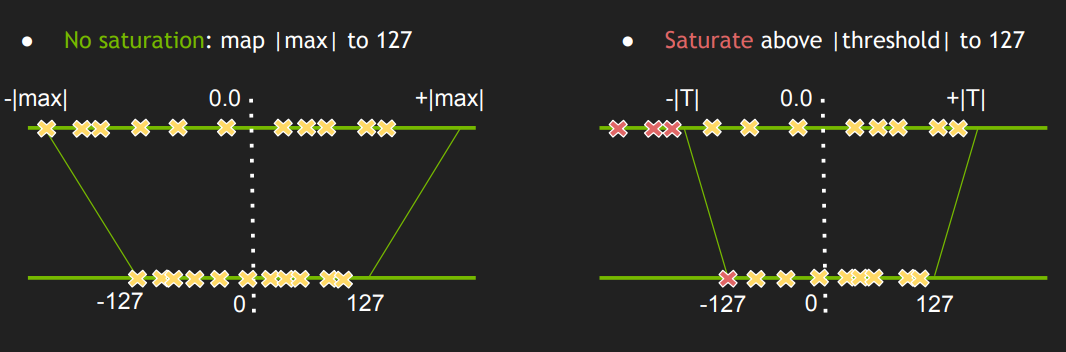
Naively, you could select a scale and offset such that no input floating point activation on a set of calibration inputs is mapped to an integer at either extreme of the range of uint8 values (-128, 127). However, in doing so we sacrifice some precision in order to accommodate extreme values. Instead, frameworks like TensorRT select scale and offset values that minimize the KL divergence between the output activations of the float32 version and int8 version of the model. This allows us to balance the tradeoff between range and precision in a principled way. As KL divergence can be viewed as a measure of information loss under a different encoding, it's a natural fit.
Information on how to apply int8 quantization to your own model's using NVIDIA's TensorRT is available below:
Layer Fusion and Graph Optimizations
Alongside floating point reduction and quantization, operation fusion presents a practical, general purpose option for more efficient prediction. The basic principle of fusion is to combine the operations performed by some layers in order to avoid redundant access of global device memory. By combining multiple operations into a single kernel we get substantially faster memory access.
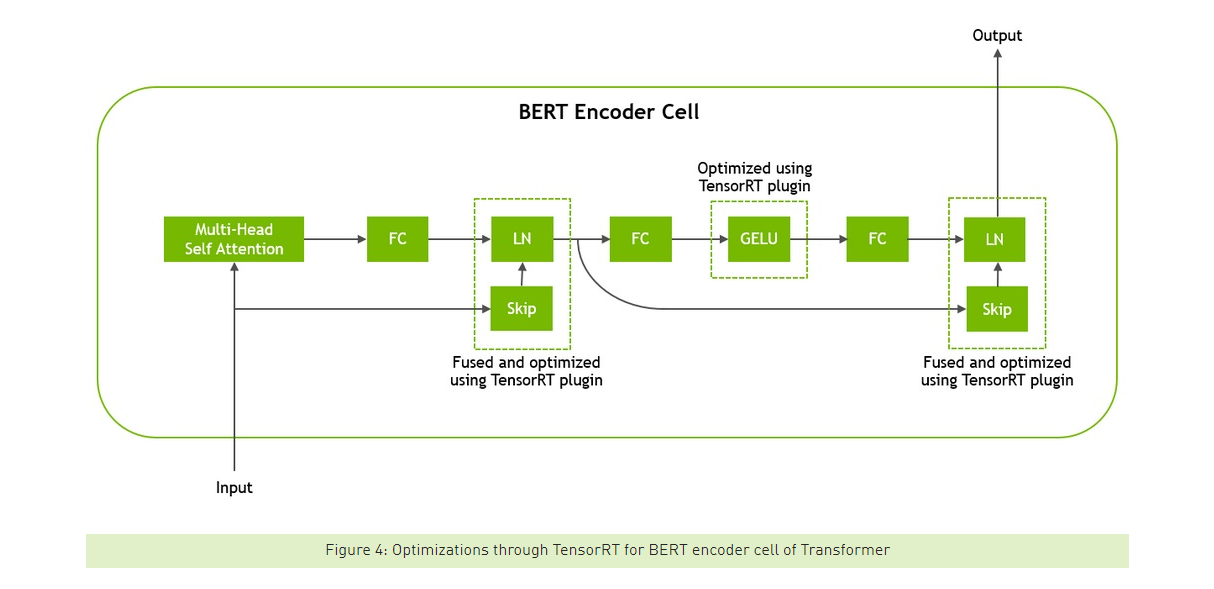
In the diagram above, this allows us to merge the addition of the skip connection with the scale and bias of the layer norm operation.
Software optimizations can also allow us to restructure some matrix multiplies to better exploit parallelism. In particular, this allows us to merge the query, key, and value projections of the self-attention layer into a single matrix multiply.
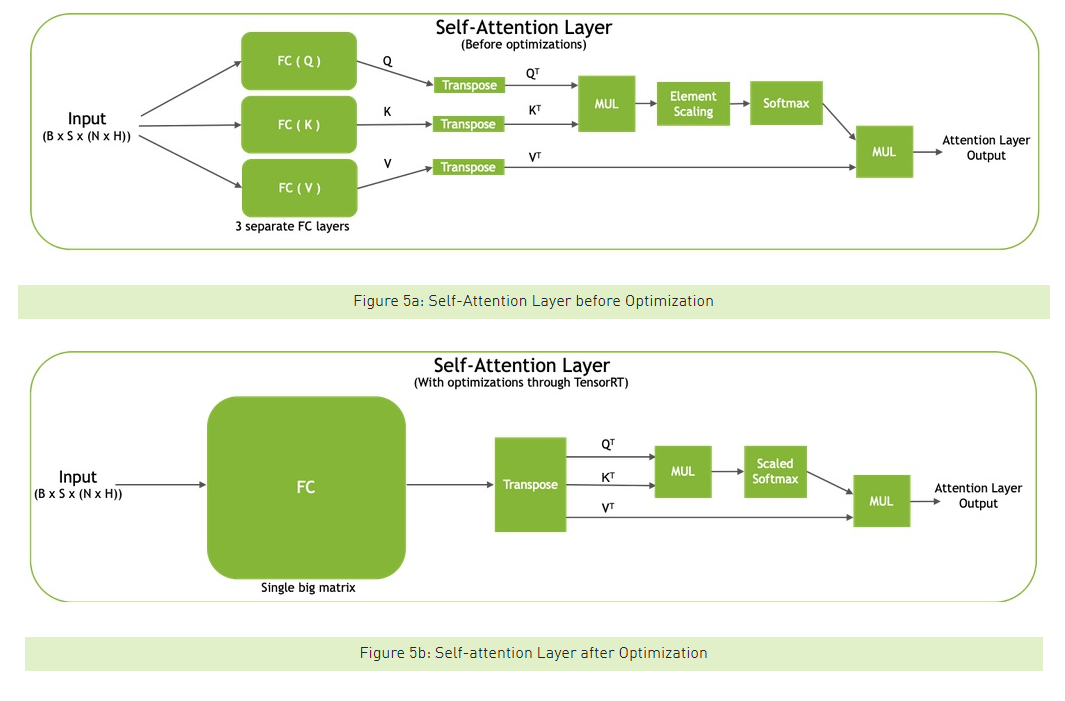
There is unfortunately little detail on the magnitude of speedups seen from this variety of graph optimization, but my best guess is that the improvement is incremental but non-negligible – on the order of a 10% difference in throughput.
Pruning
Aside from pure software efficiency options, we have a host of options available to prune neural networks and remove weights that have minimal contribution to the end model. Many pruning methods (like "Reducing Transformer Depth on Command With Structured Dropout" by Fan, et. al) require modifications to the network during pre-training in order to yield models that are adequately sparse and can be pruned after training. Other papers in the pruning literature focus on understanding the how sparse the learned connectivity patterns are without the aim of efficient prediction (for instance, "Compressing BERT: Studying the Effects of Weight Pruning on Transfer Learning" by Gorden, et. al).
While all these methods are interesting in their own right (and structured layer dropout shows significant promise for practical application), I'm particularly interested in methods that can be applied in a post-hoc fashion and still yield performance gains. This family of methods typically yield gains by exploiting the fact that only a portion of the model is necessary to solve a specific task.
Pruning for empirical performance gains requires structured sparsity. Simply zeroing out singular weights isn't sufficient to yield performance gains as we have no practical way to exploit that sparsity. So we must look to lop off larger portions of the network to yield practical performance improvements.
Pruning Attention Heads
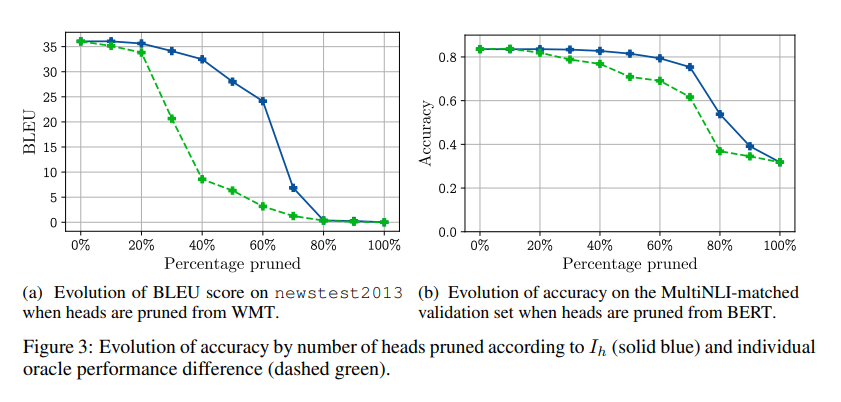
In "Are Sixteen Heads Really Better than One?", Paul Michel, Peter Levy, and Graham Neubig iterately remove heads from BERT. They use a gradient-inspection based method (where gradients are estimated on a downstream task) to estimate the important of each head and test the models robustness to removal by plotting performance as a function of the percentage of heads pruned.
$$ I_h = \lvert Att_h(x)^T \frac{\partial L(x)}{\partial Att_h(x)}\rvert$$
In practice, the authors discovered that 20 - 40% of heads could be pruned with negligible impact to accuracy.
Pruning Through Gating During Finetuning
In "Structured Pruning of a BERT-based Question Answering Model" by J.S. McCarley and Rishav Chakravarti and Avirup Sil, the authors explore a more general method of model pruning. Rather than focusing solely on the attention heads, the authors also gate each layer's inputs as well as the activations of the feed forward layer of each BERT layer.
They explore a few distinct mechanisms for selecting the elements of the network to prune, including the important measure proposed by Michel, et. al, but settle on an \(L_0\) regularization term that is applied during finetuning to encourage sparsity. To make this (\L_0\) regularization term differentiable, they employ a reparameterization trick similar to that used in variational auto-encoders.
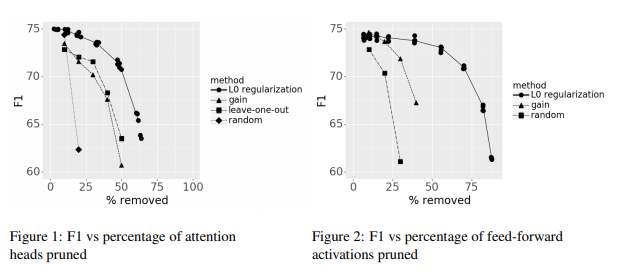
In their experiments they find that finetuning with the sparsity penalty outperforms the use of the importance estimation method used in "Are 16 Heads Really Better than 1", and find that they can additionally remove nearly 50% of feed-forward activations with negligible impact to performance on the short-question answering task they considered as a benchmark task.
To yield further gains, the author's also opt to employ the next technique on our list – "knowledge distillation".
Knowledge Distillation
Ancient History
A method first conceived by Geoffrey Hinton, Oriol Vinyals, and Jeff Dean in their 2015 work "Distilling the Knowledge in a Neural Network", knowledge distillation involves transferring the knowledge contained within one network (the "teacher") to another (the "student") via a modified loss.
Imagine first that we have access to a large pool of unlabeled samples. If we trust our teacher's predictions but the teacher model is too cumbersome or computationally expensive to use in practical settings, we could use the teacher model to predict the target class of a pool of unlabeled samples and feed these targets to the student model as supervision. If instead of producing hard targets corresponding to the class with maximum likelihood we produce a probability distribution over all possible classes, however, the student model has access to more information-rich supervision.
Intuitively, some mistakes made by the student are more reasonable than others – predicting that an image of a husky is in fact a spoon is nonsensical, but mistaking a husky for a malamute is quite reasonable. Our loss should reflect the reflect the degree of severity of an error. By penalizing the difference between the teachers predictions and student's predictions (encouraging logits to match), the student can learn meaningful information from the classes that the teacher network thought were also likely. The authors show that the large majority of the performance of the teacher network is recoverable with a meager 3% of the training data on an acoustic task.

With evidence suggesting that high parameter counts may be critical for sample efficient learning, and that training large language models to a fixed perplexity may also be more efficient in terms of wall clock time than training an equivalent compact model, methods for efficiently transferring this learned knowledge to a compressed student hold a wealth of promise.
Knowledge Distillation to Similar Model Architectures
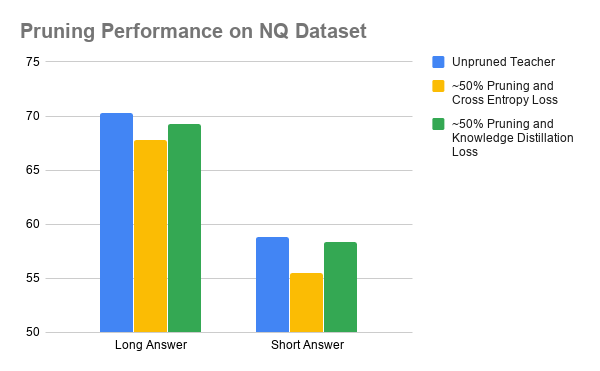
In "Structured Pruning of a BERT-based Question Answering Model" discussed earlier, knowledge distillation is used to transfer the knowledge contained in an unpruned teacher model to a pruned student. On the Natural Questions dataset, teacher performance sits at 70.3 and 58.8 F1 for Long Answer and Short Answer questions respectively. With pruning around 50% of the attention heads and feed forward activations, performance drops to 67.8 and 55.5 F1 respectively – a decrease of around 2.5 F1. If a distillation loss is used in place of a cross-entropy loss during finetuning, they recover between 1.5 and 2 F1 points and reach scores of 69.3 and 58.4.
"DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter" by Victor Sanh, Lysandre Debut, Julien Chaumond, and Thomas Wolf of Hugging Face performs knowledge distillation from BERT-base to a 6-layer BERT student during a secondary pre-training step on a masked language modeling objective. The student model (trained in a task-agnostic manner) retains an impressive 97% of model performance on the GLUE benchmark while reducing prediction time by 60%.
In TinyBERT: Distilling BERT for Natural Language Understanding, Xiaoqi Jiao, Yichun Yin, Lifeng Shang, Xin Jiang, Xiao Chen, Linlin Li, Fang Wang, and Qun Liu perform distillation from a BERT teacher to a 4 layer transformer student with hidden size 312. They distill both at pre-training time and finetuning time to yield a model that achieves 96% of BERT-base's performance on the GLUE benchmark with a 7.5x smaller package and nearly 10x faster inference times.
In "Patient Knowledge Distillation for BERT Model Compression", Siqi Sun, Yu Cheng, Zhe Gan, Jingjing Liu apply a knowledge distillation loss to many of the intermediate representations of a 12-layer BERT teacher and 6-layer BERT student to yield increased accuracy on 5/6 GLUE tasks when compared to a baseline that only applies the knowledge distillation loss to the models logits.
Knowledge Distillation to Dissimilar Model Architectures
In the papers discussed so far, the teacher model and student are share the same basic architecture and teacher weights are often used for student models' weight initializations. However, knowledge distillation loss can be applied even in scenarios where teacher and student model architectures differ dramatically.
In "Training Compact Models for Low Resource Entity Tagging using Pre-trained Language Models", Peter Izsak, Shira Guskin, and Moshe Wasserblat of Intel AI Lab distill a BERT teacher (~330M params) trained on a named entity recognition task into a dramatically more compact and efficient CNN-LSTM student (~3M params). In doing so they achieve speedups of up to 2 orders of magnitude on CPU hardware at minimal accuracy loss.
In "Distilling Transformers into Simple Neural Networks with Unlabeled Transfer Data", Subhabrata Mukherjee and Ahmed Hassan Awadallah distill BERT-Base and BERT-Large teachers into a BiLSTM student, matching the performance of the teacher in 4 classification tasks (Ag News, IMDB, Elec, and DBPedia) with a fraction of the parameter count (13M). They also observe major gains in sample efficiency thanks to distillation, requiring only 500 labeled examples per task to hit parity with the teacher (provided sufficient unlabeled data).
In "Distilling Task-Specific Knowledge from BERT into Simple Neural Networks", Raphael Tang, Yao Lu, Linqing Liu, Lili Mou, Olga Vechtomova, and Jimmy Lin report similar findings on a variety of sentence pair tasks (QQP, MNLI, etc.) using a single-layer BiLSTM with less than 1M parameters.
In "Attentive Student Meets Multi-Task Teacher: Improved Knowledge Distillation for Pretrained Models", Linqing Liu, Huan Wang, Jimmy Lin, Richard Socher, and Caiming Xiong combine multi-task learning with knowledge distillation methods to transfer the knowledge from a transformer teacher into a deep LSTM with attention. They report that the benefits from distillation stack well with generalization benefits from multi-task learning frameworks and record prediction speeds of 30X that of Patient Knowledge Distillation and 7X that of TinyBERT.
Distillation is all the rage these days and it's clear why – it's shaping up to be a likely antidote to the ever-increasing parameter counts of transformer-based language models. If we are to actualize the benefits of these GPU-hungry giants we need methods like distillation to keep prediction throughput high.
Module Replacement
The last paper on our list has the dual distinction of taking a more novel approach to model compression and also being published in conjunction with the work of modern art showcased below:

BERT-of-Theseus: Compressing BERT by Progressive Module Replacing is a work by Canwen Xu, Wangchunshu Zhou, Tao Ge, Furu Wei, and Ming Zhou. Rather than training a separate student model to minimize a knowledge distillation loss, at finetuning time BERT-of-Theseus stochastically replaces a "predecessor module" (i.e., a block of the original model) with a "successor module" (a block of the new module) with some probability each batch.
BERT of Theseus is a play on the thought experiment, the "Ship of Theseus", which asks if a ship remains the same object after being repaired and upgraded bit by bit. BERT of Theseus applies this same genre of gradual replacement to the idea of model compression.
Successor modules are cheaper versions of the predecessor modules – in this case, singular transformer layers that replace a block of 2 transformer layers. Unlike knowledge distillation, there is no loss that encourages the successor modules to mimic their predecessors. The simple fact that the successor and predecessor are used interchangeably encourages the successor to learn to mimic the behavior of the predecessor.
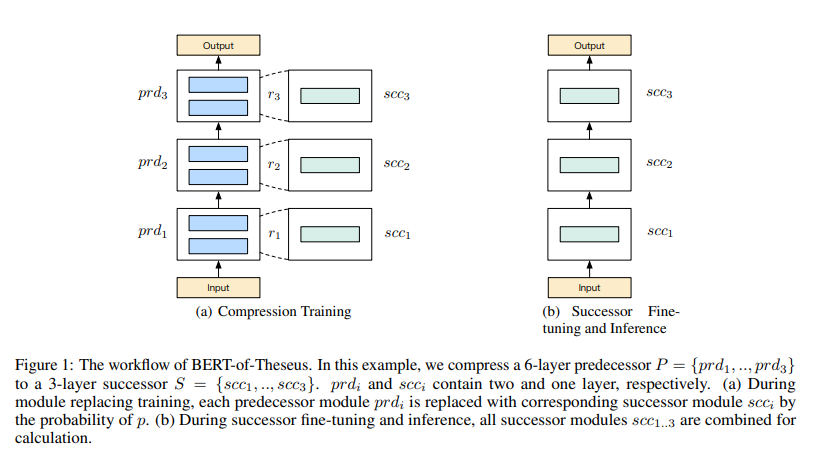
One advantage of this implicit behavior is that we no longer need to select how to weight various knowledge distillation losses with a target model loss – typically done with an alpha blending parameter of the form \(L = \alpha L_{KD} + (1-\alpha) L_{CE}\). Unlike TinyBERT, there is no secondary pre-training step – the compression is performed concurrently with downstream finetuning. Finally, the progressive module replacement method is also applicable across model architectures – it doesn't exploit any particular feature of transformer models in its design.
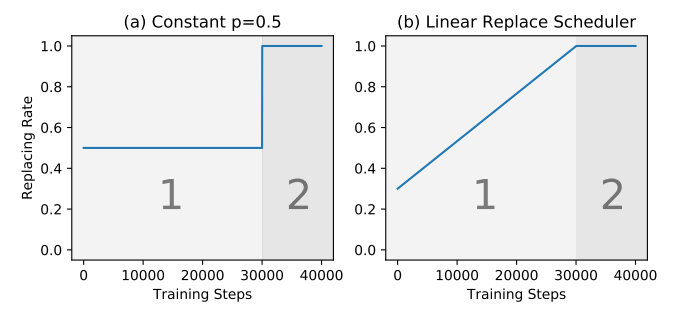
The authors experiment with a linear learning rate schedule and find that increasing the module replacement rate linearly over time outperforms a constant replacement rate.
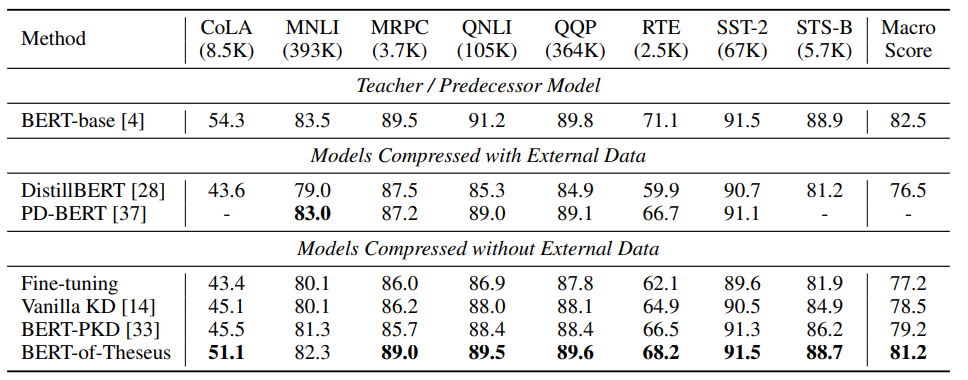
To test the robustness of their method, the authors use "Theseus Compression during application of BERT-base to the GLUE benchmark and handily outperformed several knowledge distillation based methods, often lagging behind BERT-base by less than 1 point while compressing the original model to 50% its size.
Part of the reason I find this line of work into progressive module replacement enticing is that I imagine it opens up the gate to experiment with other methods for increasing model throughput that would typically require re-training for scratch. For independent researchers and smaller companies it's often intractable to retrain transformer models from scratch, so it's hard to leverage papers that put forward useful ideas for increasing model efficiency but don't release a pre-trained model.
I'm eager to see whether the progressive module replacement idea proposed by BERT-of-Theseus allows the replacement of a pre-trained attention module with the shared key and value version proposed in "Fast Transformer Decoding: One Write-Head is All You Need", or perhaps a sparse attention equivalent. More broadly, we need to continue developing methods that exploit the large amounts of computation expended during language model pre-training but also allow us to make post-hoc modifications to adapt these expensive models to task-specific requirements. I'm excited to see how future research builds on this unique foundation.
Further Reading
If you're interested in learning more about methods for more efficient prediction for BERT-based models, you might enjoy:
- Compressing Large-Scale Transformer-Based Models: A Case Study on BERT by Prakhar Ganesh , Yao Chen , Xin Lou , Mohammad Ali Khan, Yin Yang , Deming Chen , Marianne Winslett , Hassan Sajjad and Preslav Nakov
- All the Ways You Can Compress BERT – a blog post by Michael Gordon I referenced often while writing this post.




